Trees

In this tutorial, we’ll be covering Binary Trees, Binary Search Trees, and K-ary Trees. We will review some common terminology that is shared amongst all of the trees and then dive into specifics of the different types. Common Terminology

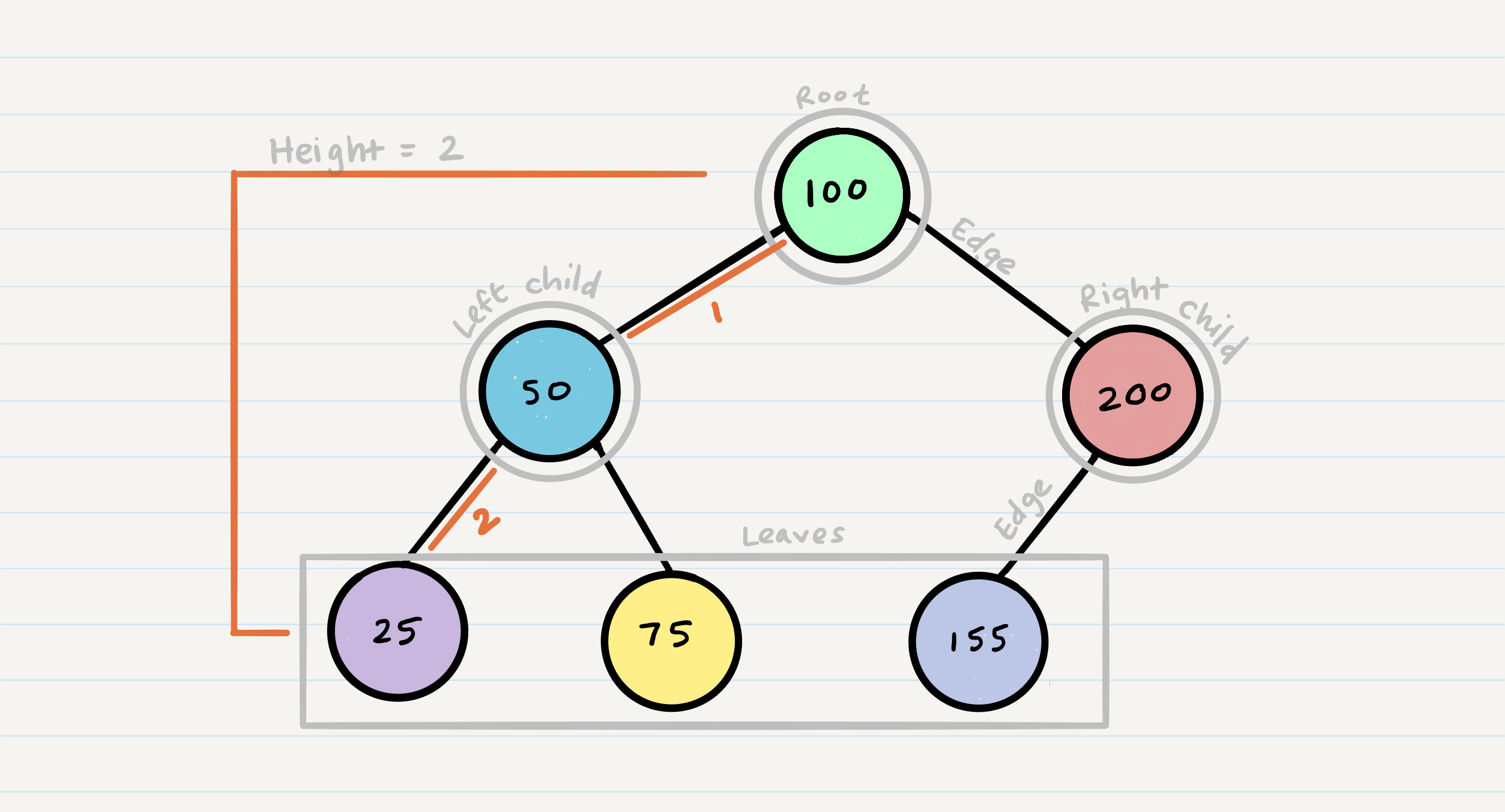
1. Node - A Tree node is a component which may contain it’s own values, and references to other nodes
2. Root - The root is the node at the beginning of the tree
3. K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2.
4. Left - A reference to one child node, in a binary tree
5. Right - A reference to the other child node, in a binary tree
6. Edge - The edge in a tree is the link between a parent and child node
7. Leaf - A leaf is a node that does not have any children
8. Height - The height of a tree is the number of edges from the root to the furthest leaf

Sample Tree

Traversals

An important aspect of trees is how to traverse them. Traversing a tree allows us to search for a node, print out the contents of a tree, and much more! There are two categories of traversals when it comes to trees:

1. Depth First
2. Breadth First

Depth First

Depth first traversal is where we prioritize going through the depth (height) of the tree first. There are multiple ways to carry out depth first traversal, and each method changes the order in which we search/print the root. Here are three methods for depth first traversal:

1. Pre-order: root » left » right
2. In-order: left » root » right
3. Post-order: left » right » root

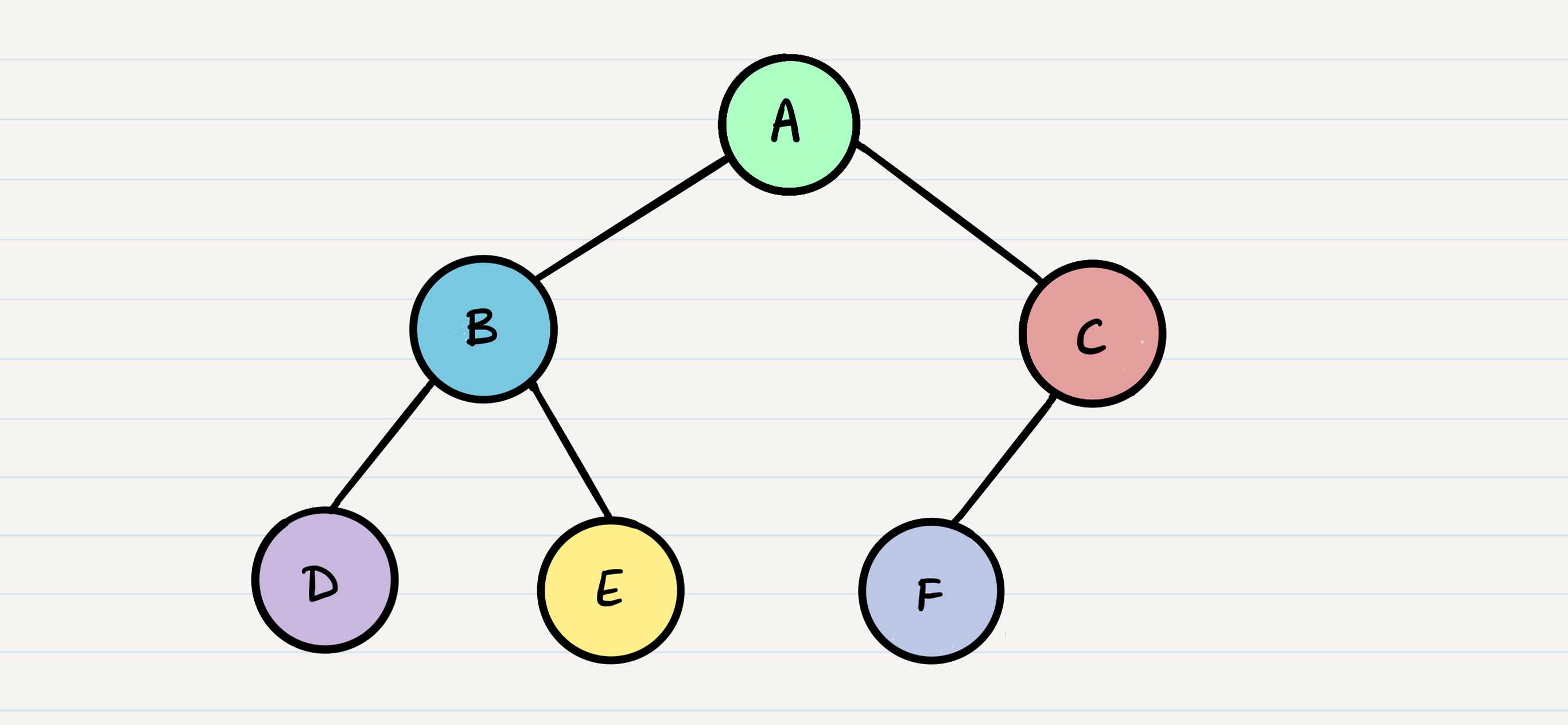
• Given the sample tree above, our traversals would result in different paths:

1. Pre-order: A, B, D, E, C, F
2. In-order: D, B, E, A, F, C
3. Post-order: D, E, B, F, C, A

The most common way to traverse through a tree is to use recursion. With these traversals, we rely on the call stack to navigate back up the tree when we have reached the end of a sub-path.

Breadth First

Breadth first traversal iterates through the tree by going through each level of the tree node-by-node. So, given our starting tree one more time:

Our output using breadth first traversal is now:

Output: A, B, C, D, E, F

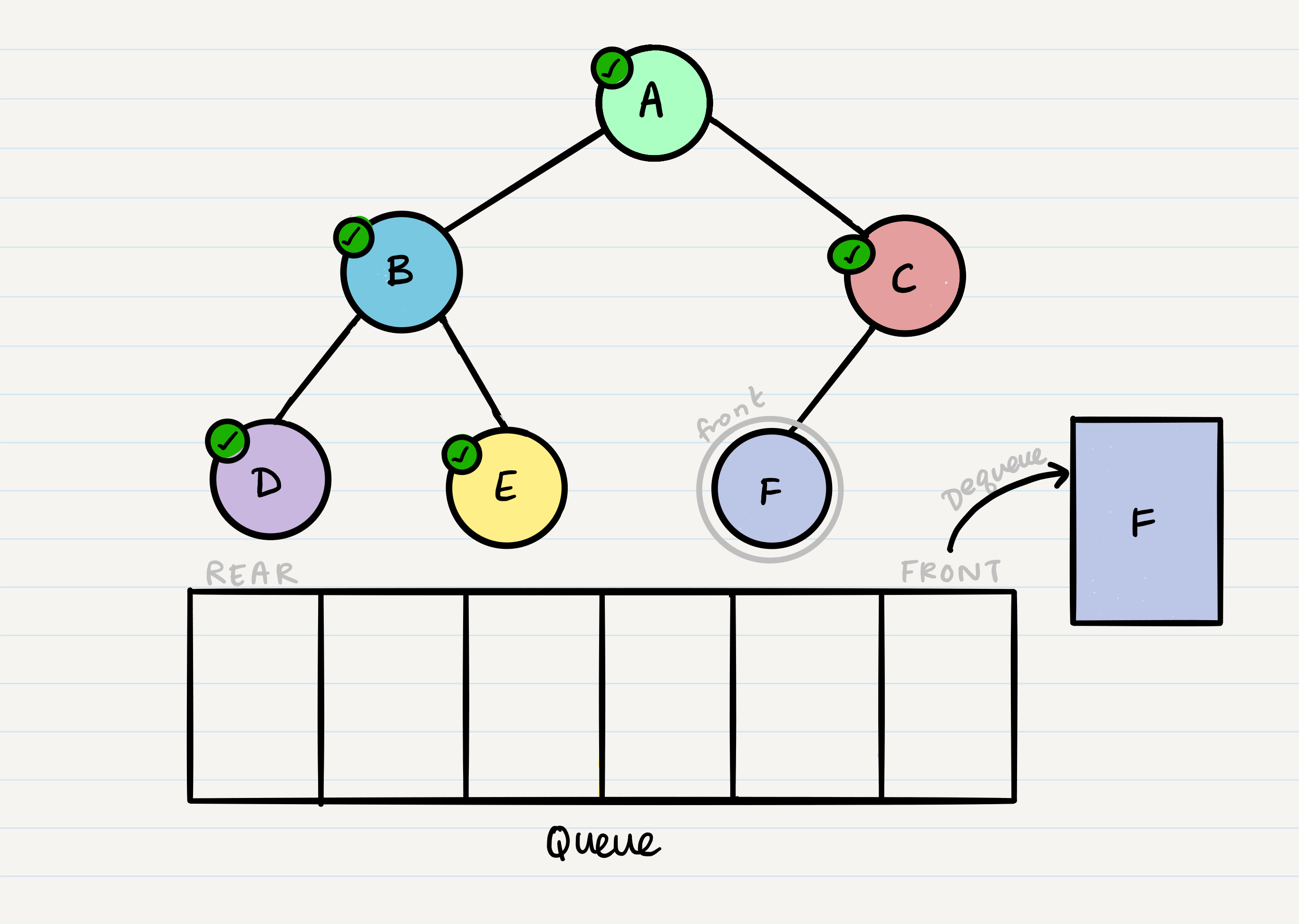
Traditionally, breadth first traversal uses a queue (instead of the call stack via recursion) to traverse the width/breadth of the tree. Let’s break down the process.

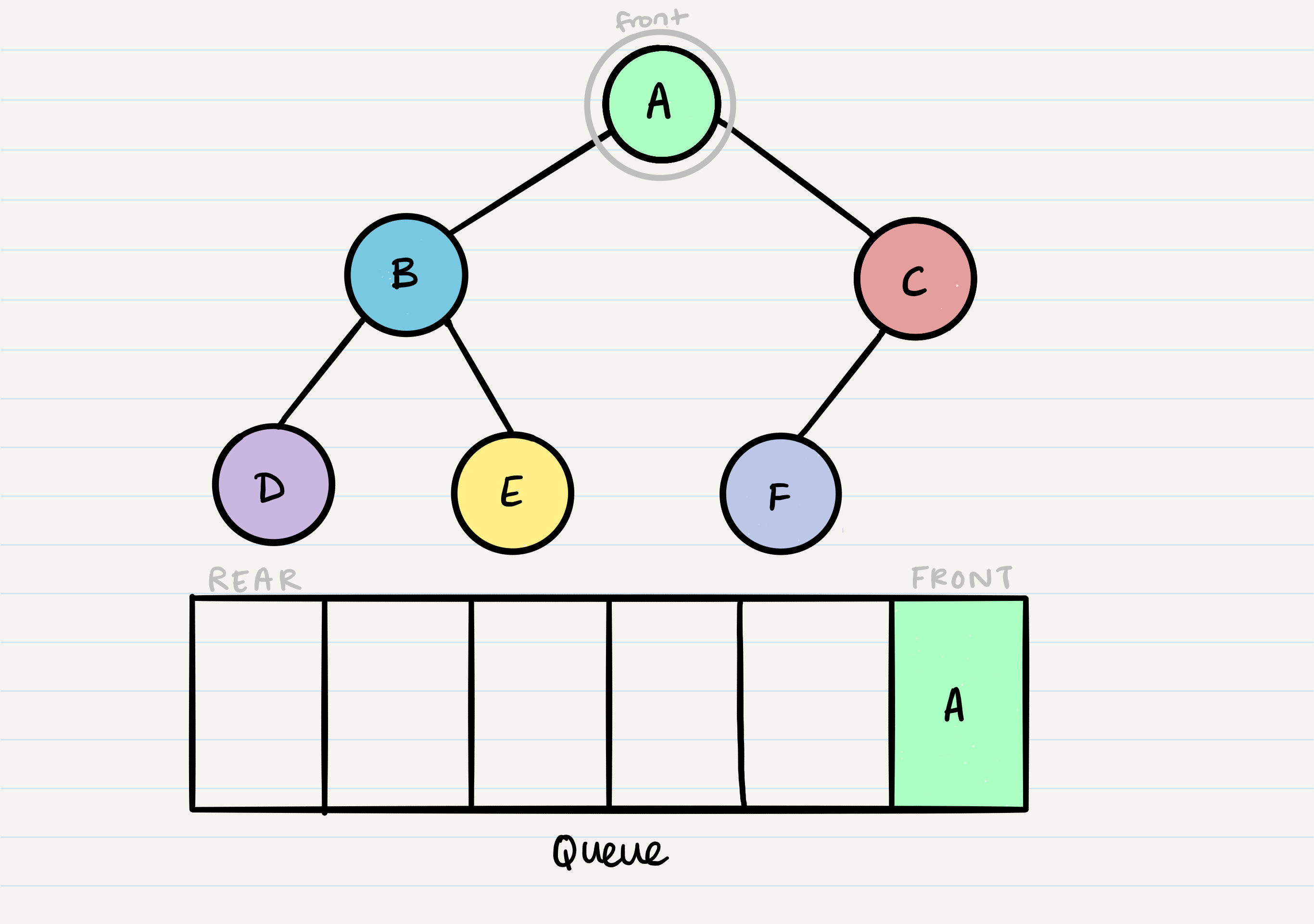
Given our starting tree shown above, let’s start by putting the root into the queue:

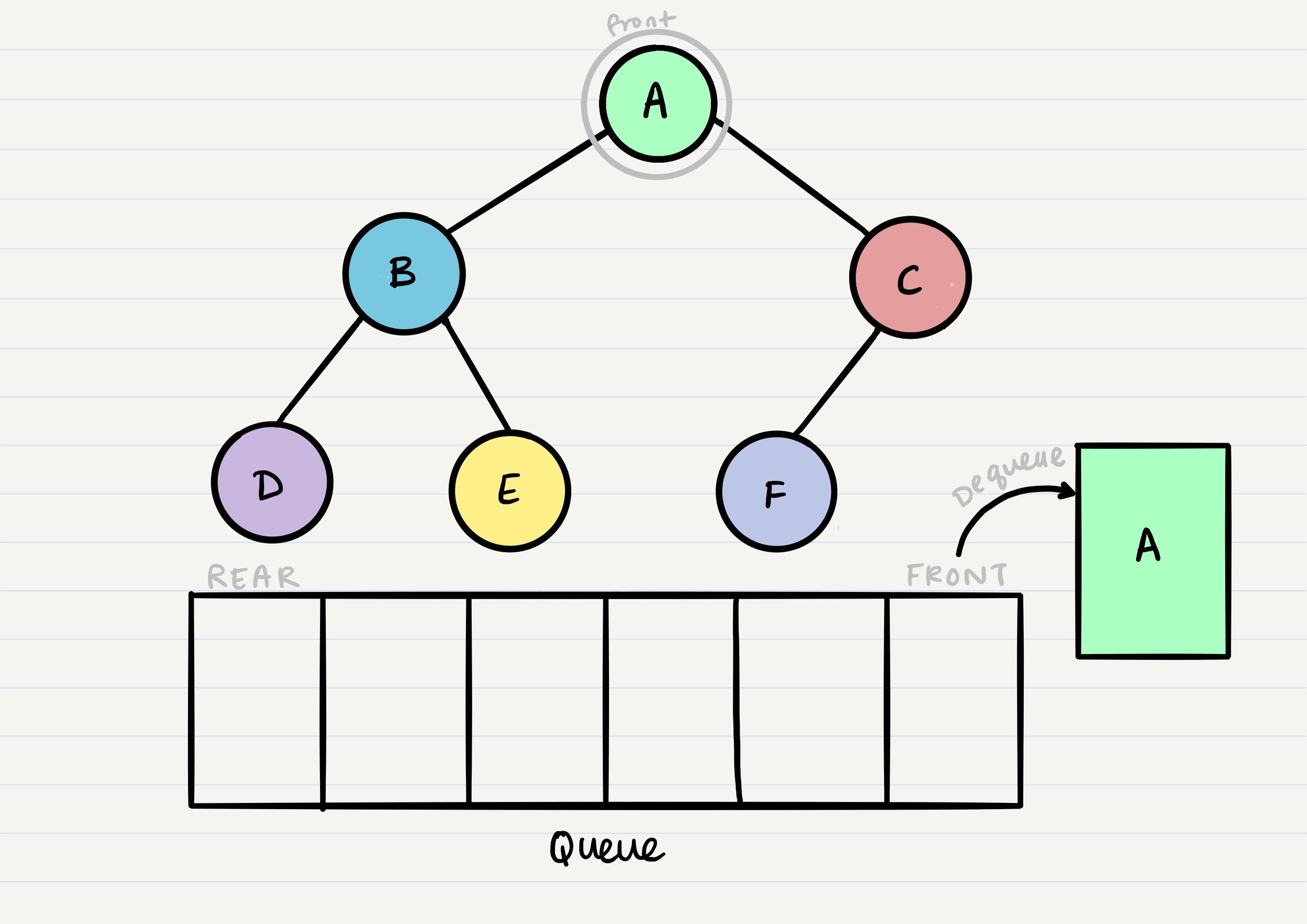
Now that we have one node in our queue, we can dequeue it and use that node in our code.

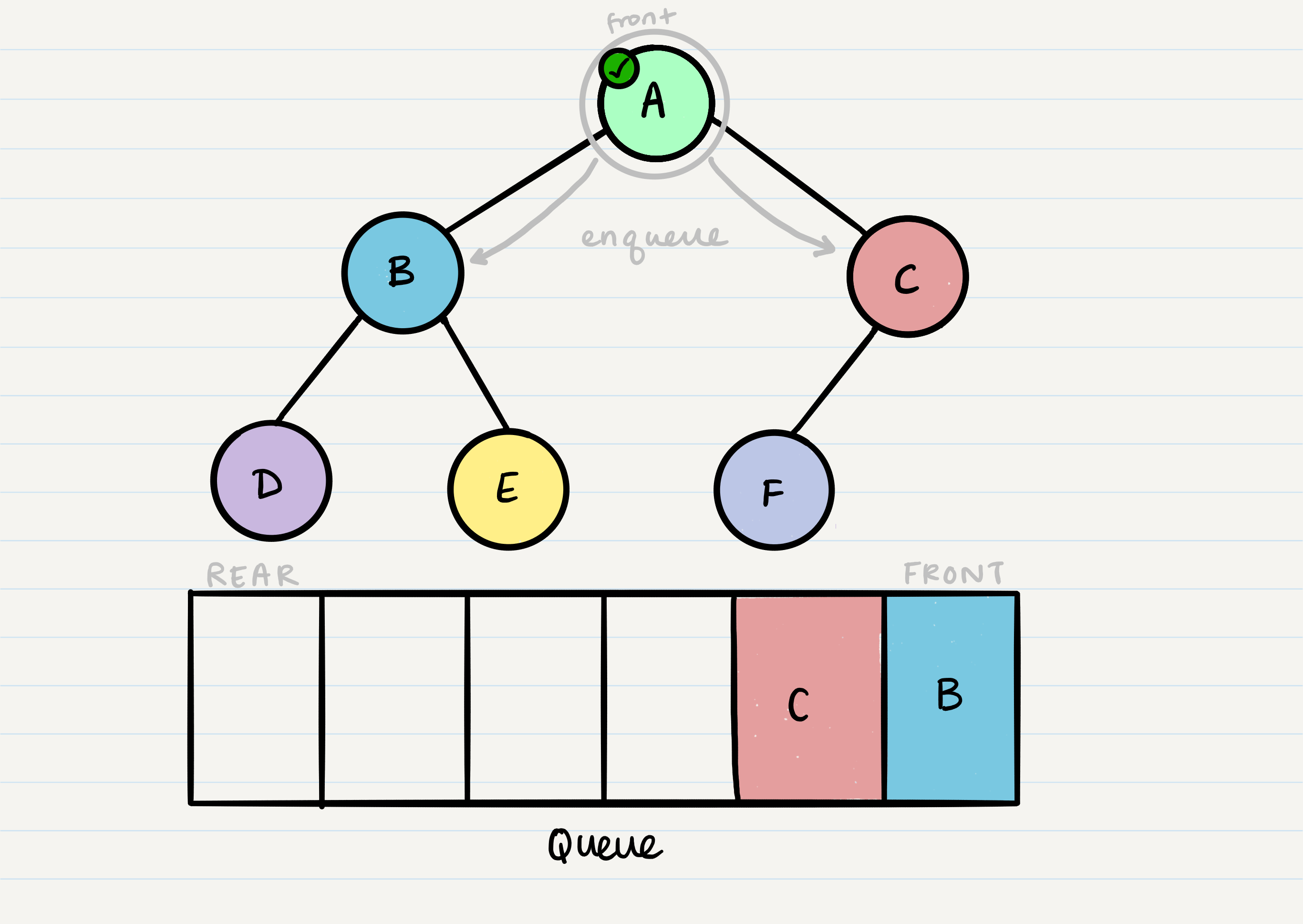
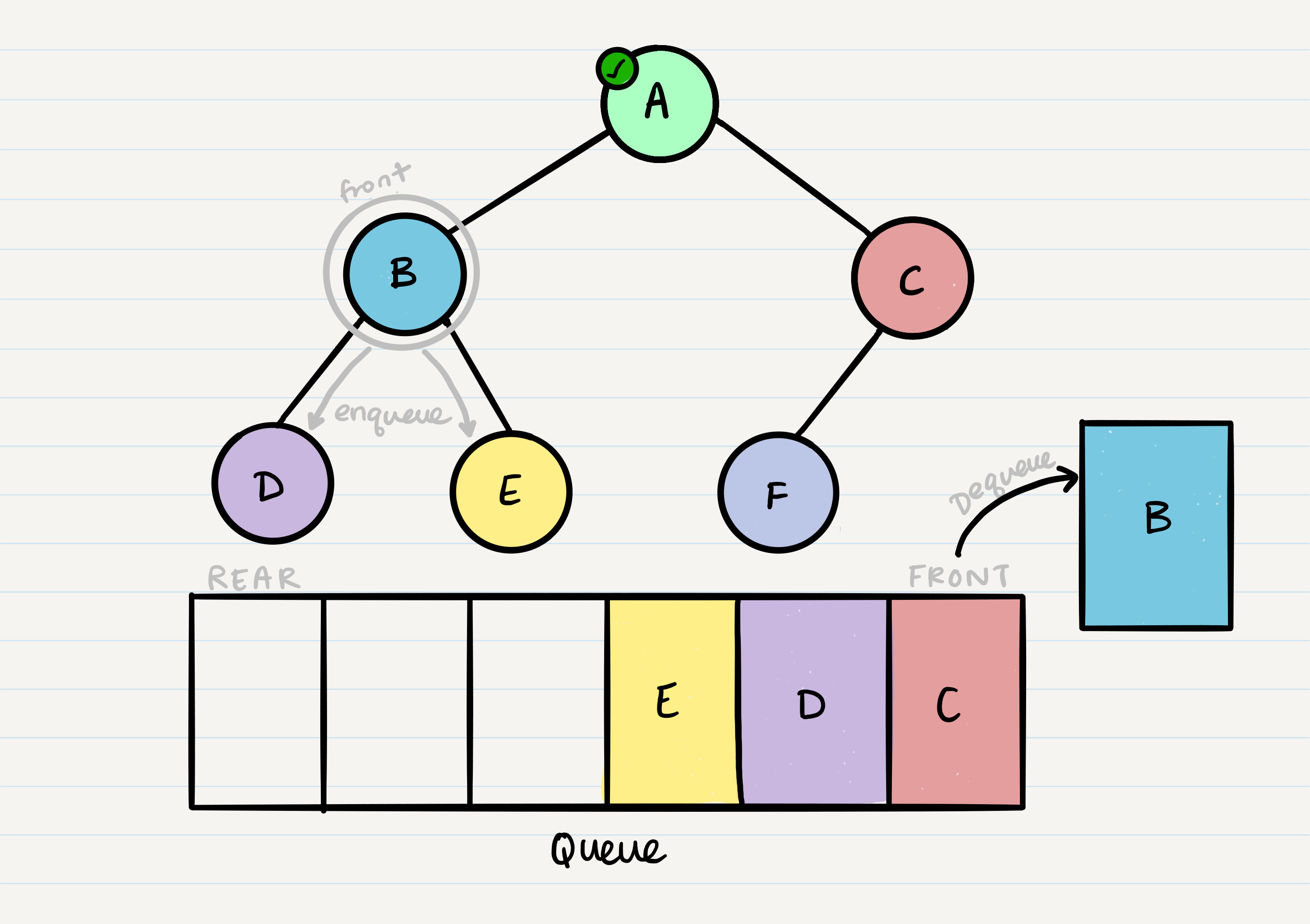
From our dequeued node A, we can enqueue the left and right child (in that order).

This leaves us with B as the new front of our queue. We can then repeat the process we did with A: Dequeue the front node, enqueue that node’s left and right nodes, and move to the next new front of the queue.

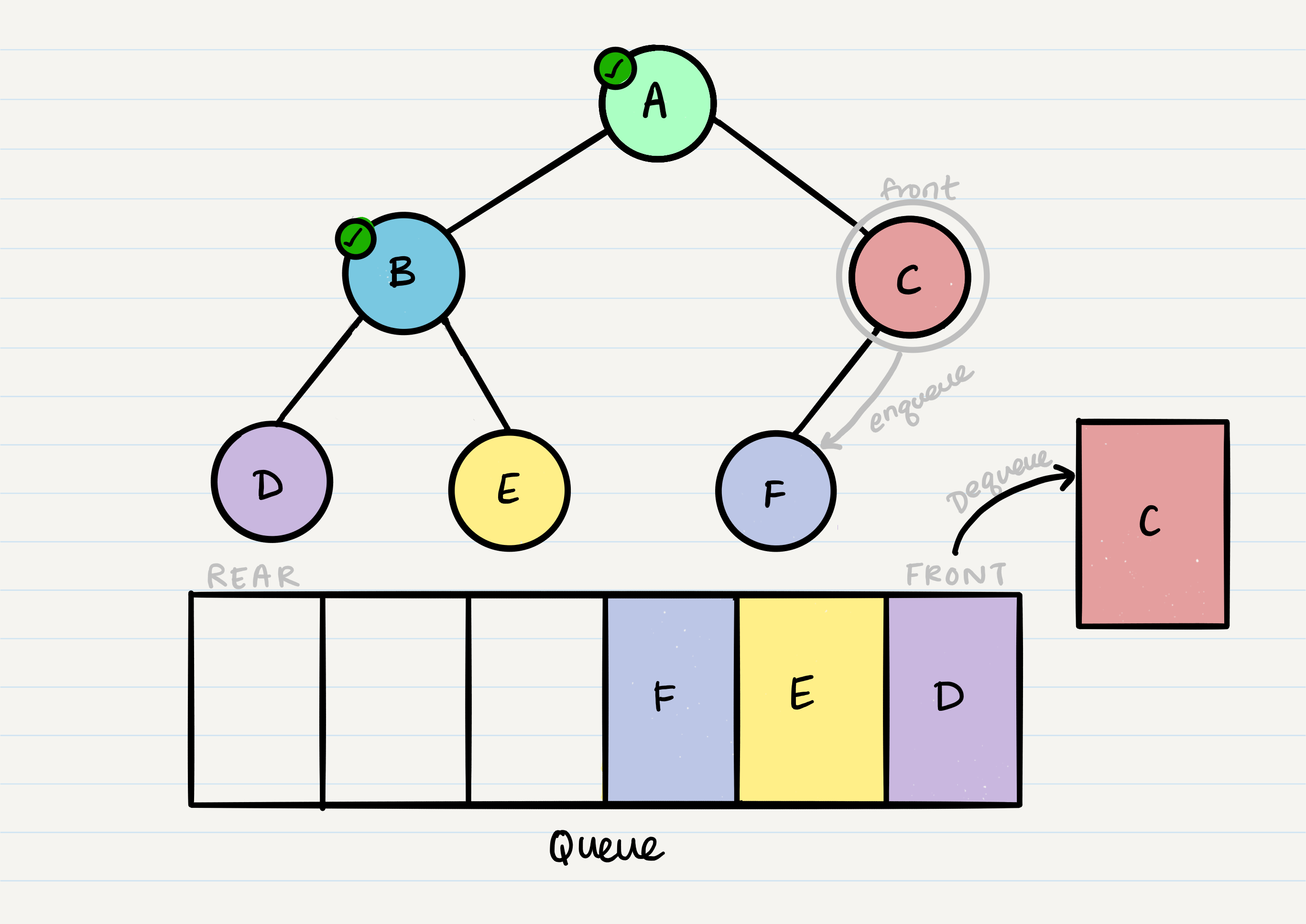
Now our front is C, so we repeat the dequeue + enqueue children process:

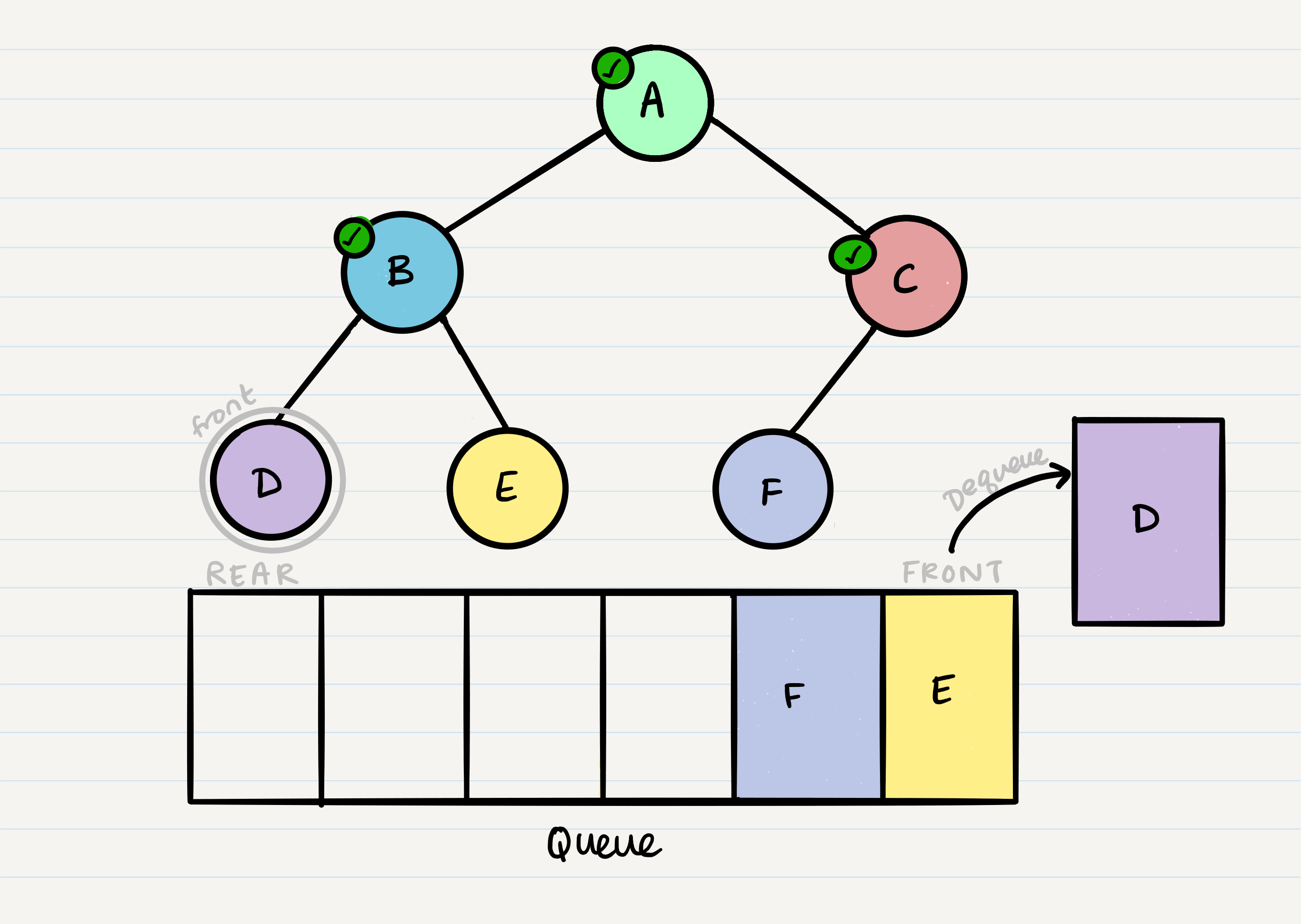
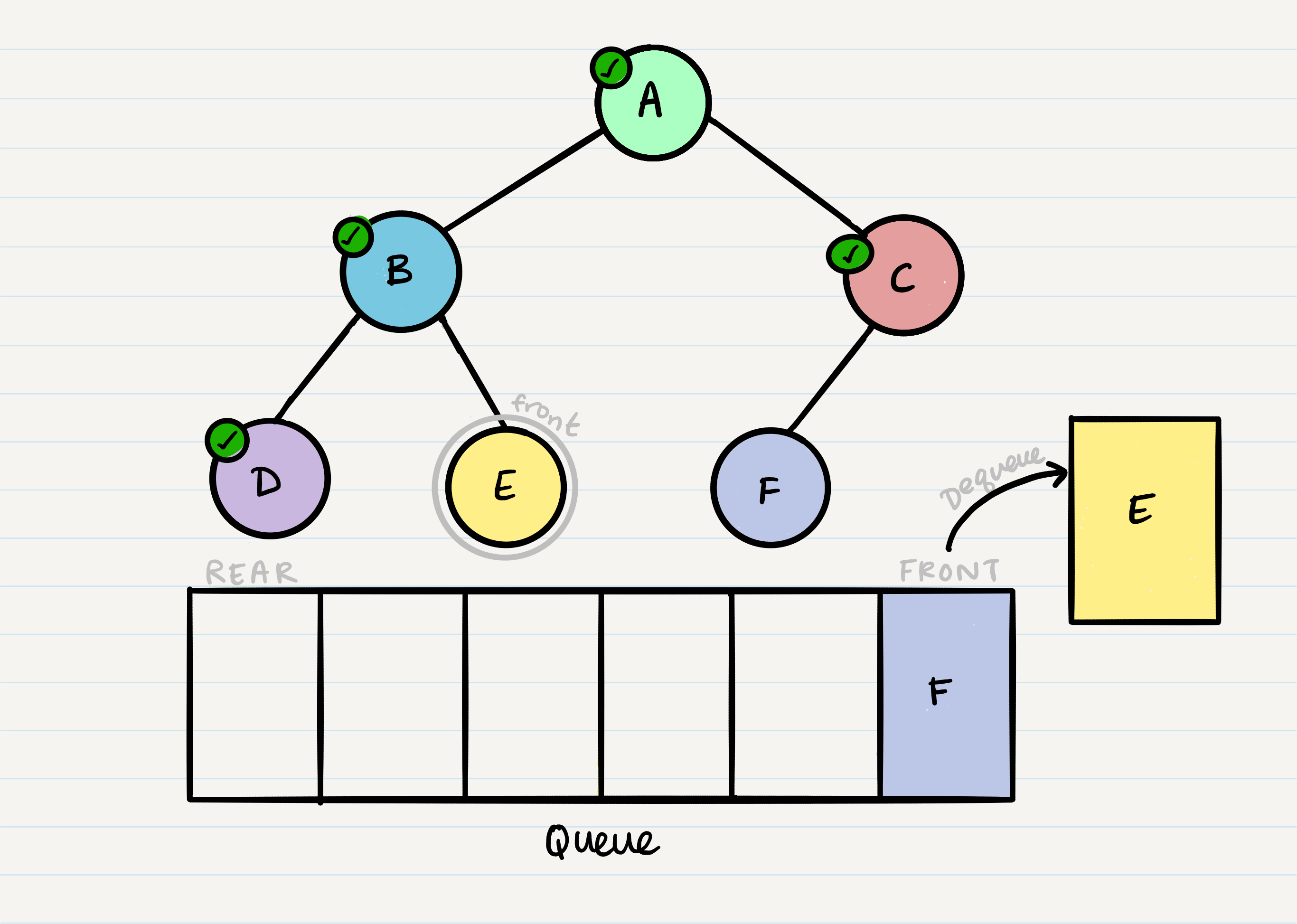
And we continue onwards. When we reach a node that doesn’t have any children, we just dequeue it without any further enqueue.

References

• Trees Read full article)

Main page